深度学习,手势识别
CNN卷积神经网络
参考链接
一维卷积Conv1d
二维卷积Conv2d
三维卷积Conv3d
融合层Merge 分离层lambda
lambda 将Input输入层分隔
Merge 融合层
ANN
CNN后面接LSTM
机器学习指标
召回率F1
机器学习算法分类
TCN
DenseNet
论文地址
Keras实现DenseNet结构
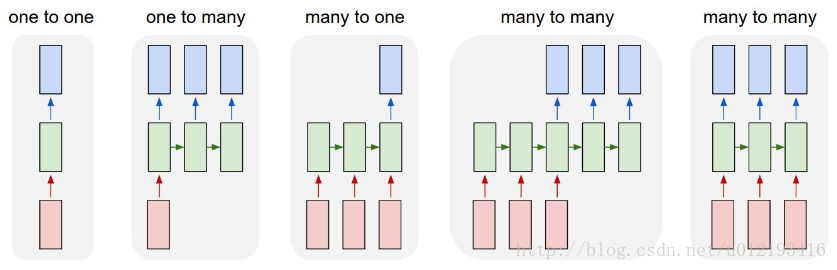
LSTM RNN
keras中TimeDistributed的用法
计算top-1 err和计算top-5 err
top1就是你预测的label取最后概率向量里面最大的那一个作为预测结果,你的预测结果中概率最大的那个类必须是正确类别才算预测正确。而top5就是最后概率向量最大的前五名中出现了正确概率即为预测正确
Batch Normalization
作者认为:网络训练过程中参数不断改变导致后续每一层输入的分布也发生变化,
而学习的过程又要使每一层适应输入的分布,因此我们不得不降低学习率、小心地初始化。
作者将分布发生变化称之为 internal covariate shift。
Batch Normalization
GlobalAveragePooling2D层
就是在卷积层之后,用GAP替代FC全连接层。有两个有点:一是GAP在特征图与最终的分类间转
换更加简单自然;二是不像FC层需要大量训练调优的参数,降低了空间参数会使模型更加健壮,抗过拟合效果更佳
YOLOV3
自定义激活函数
Neual Network可视化工具
keras-vis
什么使用local connected layer,fully connected layer
当数据集具有全局的局部特征分布时,也就是说局部特征之间有较强的相关性,适合用全卷积。在不同的区域有不同的特征分布时,适合用local-Conv
BP反向传播
Python使用numpy实现BP神经网络
优点:能比较鲁棒性地评估模型在未知数据上的性能
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| $
$ from keras.models import Sequential
$ from keras.layers import Dense
$ from sklearn.model_selection import StratifiedKFold
$ import numpy
$
$ seed = 7
$ numpy.random.seed(seed)
$
$ dataset = numpy.loadtxt("pima-indians-diabetes.csv", delimiter=",")
$
$ X = dataset[:,0:8]
$ Y = dataset[:,8]
$
$ kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=seed)
$ cvscores = []
$ for train, test in kfold.split(X, Y):
$
$ model = Sequential()
$ model.add(Dense(12, input_dim=8, activation='relu'))
$ model.add(Dense(8, activation='relu'))
$ model.add(Dense(1, activation='sigmoid'))
$
$ model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
$
$ model.fit(X[train], Y[train], epochs=150, batch_size=10, verbose=0)
$
$ scores = model.evaluate(X[test], Y[test], verbose=0)
$ print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))
$ cvscores.append(scores[1] * 100)
$ print("%.2f%% (+/- %.2f%%)" % (numpy.mean(cvscores), numpy.std(cvscores)))
|
K-flod cross validation
将数据集分成k份,每一轮用其中(k-1)份做训练而剩余1份做验证,以这种方式执行k轮,得到k个模型.将k次的性能取平均,作为该算法的整体性能.k一般取值为5或者10
缺点:计算复杂度较大.因此,在数据集较大,模型复杂度较高,或者计算资源不是很充沛的情况下,可能不适用,尤其是在训练深度学习模型的时候
Keras自定义层
https://keras.io/guides/making_new_layers_and_models_via_subclassing/
自定义激活函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| $ import os
$ from keras import backend as K
$ from keras.layers import Activation,Conv2D
$ from keras.utils.generic_utils import get_custom_objects
$ os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
$
$
$ def swish(x):
$ '''
$ x:每个值
$ '''
$ return (K.sigmoid(x) * x)
$ get_custom_objects().update({'swish': Activation(swish)})
$
$
$ net = Activation("swish")(net)
$
$ net = (......,activation='swish')(net)
|
1
2
3
4
5
6
7
8
9
| $ from keras import backend as K
$ from keras.utils.generic_utils import get_custom_objects
$
$ def custom_activation(x):
$ return (K.sigmoid(x) * 5) - 1
$
$ get_custom_objects().update({'custom_activation': Activation(custom_activation)})
$
$ model.add(Activation(custom_activation))
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| $ from keras import backend as K
$ from keras.layers.core import Lambda
$ from keras.engine import Layer
$
$
$ def sigmoid_relu(x):
$ """
$ f(x) = x for x>0
$ f(x) = sigmoid(x)-0.5 for x<=0
$ """
$ return K.relu(x)-K.relu(0.5-K.sigmoid(x))
$
$
$ def lambda_activation(x):
$ """
$ f(x) = max(relu(x),sigmoid(x)-0.5)
$ """
$ return K.maximum(K.relu(x),K.sigmoid(x)-0.5)
$
$
$ class My_activation(Layer):
$ """
$ f(x) = x for x>0
$ f(x) = alpha1 * x for theta<x<=0
$ f(x) = alpha2 * x for x<=theta
$ """
$ def __init__(self,theta=-5.0,alpha1=0.2,alpha2=0.1,**kwargs):
$ self.theta = theta
$ self.alpha1 = alpha1
$ self.alpha2 = alpha2
$ super(My_activation,self).__init__(**kwargs)
$ def call(self,x,mask=None):
$ fx_0 = K.relu(x)
$ fx_1 = self.alpha1*x*K.cast(x>self.theta,K.floatx())*K.cast(x<=0.0,K.floatx())
$ fx_2 = self.alpha2*x*K.cast(x<=self.theta,K.floatx())
$ return fx_0+fx_1+fx_2
$ def get_output_shape_for(self, input_shape):
$
$ return input_shape
$
$
$ class Trainable_activation(Layer):
$ """
$ f(x) = x for x>0
$ f(x) = alpha1 * x for theta<x<=0
$ f(x) = alpha2 * x for x<=theta
$ """
$ def __init__(self,init='zero',theta=-5.0,**kwargs):
$ self.init = initializations.get(init)
$ self.theta = theta
$ super(Trainable_activation,self).__init__(**kwargs)
$ def build(self,input_shape):
$ self.alpha1 = self.init(input_shape[1:],name='alpha1')
$ self.alpha2 = self.init(input_shape[1:],name='alpha2')
$ self.trainable_weights = [self.alpha1,self.alpha2]
$ def call(self,x,mask=None):
$ fx_0 = K.relu(x)
$ fx_1 = self.alpha1*x*K.cast(x>self.theta,K.floatx())*K.cast(x<=0.0,K.floatx())
$ fx_2 = self.alpha2*x*K.cast(x<=self.theta,K.floatx())
$ return fx_0+fx_1+fx_2
$ def get_output_shape_for(self, input_shape):
$
$ return input_shape
$
|
使用时
1
2
3
4
| $ model.add(Activation(sigmoid_relu))
$ model.add(Lambda(lambda_activation))
$ model.add(My_activation(theta=-5.0,alpha1=0.2,alpha2=0.1))
$ model.add(Trainable_activation(init='normal',theta=-5.0))
|
强化学习 Enforce learning
https://www.jianshu.com/p/e037d42ab6b1
机器学习参数的难题
(1)参数太多,如果训练数据集有限,很容易产生过拟合;
(2)网络越大、参数越多,计算复杂度越大,难以应用;
(3)网络越深,容易出现梯度弥散问题(梯度越往后穿越容易消失),难以优化模型
SE-Net
对于channel维度的特征融合,卷积操作基本上默认对输入特征图的所有channel进行融合。而MobileNet网络中的组卷积(Group Convolution)和深度可分离卷积(Depthwise Separable Convolution)对channel进行分组也主要是为了使模型更加轻量级,减少计算量
参考书籍
Deep Learning for Time Series Forecasting
该作者网站
Hikey970

